なんちゃって自作体温計の製作
 2020/5/6
2020/5/6  2021/7/1
2021/7/1
新型コロナウイルスの影響で、週1回の卓球教室は自粛営業となり、体育館でのサークルも中止となりました。もちろん、卓球の試合もありません。
勤めている会社では時差出勤、在宅勤務が導入され、体調管理を行うため毎日の検温の推奨がありました。
自宅には6年ほど前に購入したオムロン社製 MC-246という電子体温計が1台あり家族で使っていますが、やはりもう1台欲しいなぁと思い店舗に行くと見当たりません。マスクと同様に品切れ状態が続いているようです。
なければ作ってみようかと思い、手持ちにある Arduino nanoマイコンで検討をしました。
オムロン社製 MC-246 の仕様
オムロン社製 MC-246です。
仕様を調べてみました。
| 名称 | オムロン電子体温計 MC-246 けんおんくん |
|---|---|
| 感温部 | サーミスタ |
| 体温表示 | 3桁+℃表示、0.1℃毎 |
| 測定精度 | ±0.1℃(標準室温23℃) |
| 測定範囲 | 32.0℃~42.0℃ |
電子体温計の感温部には、サーミスタという温度によって抵抗値が変化する素子が使われています。また、予測式と実測式があり予測後、実測方式に変わり、約10分ほどでより正確な測定ができるようです。予測式はそのアルゴリズムがまったくわからないので、普通に実測式で考えてみます。
サーミスタは様々な種類があり、一般的に NTC(negative temperature coefficient)サーミスタが使われていることがわかりました。NTCサーミスタは負の温度特性があり、温度が上昇すると抵抗値が下がります。
いつものように、秋月電子通商のサイトを見ると、NTCサーミスタが販売されていましたので購入し、サーミスタ抵抗値計算方法の説明もあり、これで検討をしました。
NTCサーミスタ(温度検知・温度補償用)10KΩ
| メーカー | 村田製作所 |
|---|---|
| 型番 | NXFT15XH103FA2B050 |
| 抵抗値 | 10KΩ±1%(25℃) |
| B定数 | 3380K±1%(25-50℃) |
サーミスタのある温度における抵抗値の計算方法
サーミスタのある温度における抵抗値の計算方法は、以下のように解説されています。
$T_0$ ℃での抵抗値が $R_0$ Ωのサーミスタにおける、温度 $T$ ℃の抵抗値は次式で算出することができます。$B$ 定数の単位が $K$(ケルビン)なので、次式では温度 $T$ および $T_0$ に273を足して換算しています。
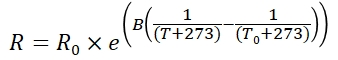
なにやら、$e$ という記号に指数があり、その中の $T$ ℃に温度を入れるとサーミスタの抵抗値が計算できる式です。$e$ はネイピア数といい、自然対数の底と呼ばれています。また、$K$(ケルビン)という記号もあり、これは絶対温度を表しています。
絶対温度とは「原子・分子が熱運動でほとんどなくなる温度を0K」といい、私達が通常使っている摂氏温度(セルシウス温度)は「1気圧のもとで氷が溶ける温度を0℃、水が沸騰する温度を100℃」と決めた温度です。絶対温度を摂氏温度に変換しているのですね。そういえば小学校のときに学んだ記憶があります。
昔、電験三種(第三種電気主任技術者)の勉強をしていたときに、オイラーの公式、ヒートポンブの熱力学で学んだことを思い出しましたが、未だによく理解していません。
ここで知りたいのは、サーミスタの抵抗値から $T$ ℃の温度を知りたいので式を展開していきます。
$e$ の指数にある $B$ を除く分数同士の引き算を一旦、見やすいように $C$ とおきます。
\(C=\left(\cfrac{1}{(T+273)}-\cfrac{1}{(T_0+273)}\right)\)
\(R=R_0\times e^{BC}\)
\(e^{BC}=\cfrac{R}{R_0}\)
指数関数から対数関数へ変換します。
\(BC=\log(\cfrac{R}{R_0})\)
\(C=\cfrac{\log(\cfrac{R}{R_0})}{B}\)
$C$ を元に戻します。
\(\left(\cfrac{1}{(T+273)}-\cfrac{1}{(T_0+273)}\right)=\cfrac{\log(\cfrac{R}{R_0})}{B}\)
\(\cfrac{1}{(T+273)}=\cfrac{\log(\cfrac{R}{R_0})}{B}+\cfrac{1}{(T_0+273)}\)
\(T+273=\cfrac{1}{\cfrac{\log(\cfrac{R}{R_0})}{B}+\cfrac{1}{(T_0+273)}}\)
\(T=\cfrac{1}{\cfrac{\log(\cfrac{R}{R_0})}{B}+\cfrac{1}{(T_0+273)}}-273\)
これで、サーミスタの抵抗値 $R$ から 温度 $T$ を求めることができました。本当にあっているのかな?と不安になったので、Excelで確認してみます。
温度 $T$ ℃ に25.0℃、26.0℃というふうに数値を入れて、サーミスタ抵抗 $R$ Ωを求めていきます。$e$ のネイピア数の計算には、EXP関数($e$ を底とする数値のべき乗を返す関数)を使います。このように温度が上昇するとサーミスタの抵抗値は下がってきます。
今度は展開した式があっているか確認するため、サーミスタ抵抗 $R$ Ωから温度 $T$ ℃を求めます。これには、LN関数($e$ を底とする対数(自然対数)を返す関数)を使います。
このように温度 $T$ ℃から求めたサーミスタ抵抗 $R$ Ωと、サーミスタ抵抗 $R$ Ωから求めた温度 $T$ ℃は同じ値になります。ちゃんと展開されていますね。
B定数:$B=3380$、基準温度:$T_0=25$、基準抵抗:$R_0=10000$
| 温度 T ℃ | サーミスタ抵抗 R Ω | Rから求めた温度 ℃ |
|---|---|---|
| 25.0 | 10000 | 25.0 |
| 26.0 | 9628 | 26.0 |
| 27.0 | 9272 | 27.0 |
| 28.0 | 8931 | 28.0 |
| 29.0 | 8605 | 29.0 |
| 30.0 | 8293 | 30.0 |
サーミスタ抵抗 $R$ Ωから温度 $T$ ℃を求めることができました。
サーミスタ抵抗の基準温度25℃から、電子体温計の最大測定温度42.0℃までのサーミスタ温度特性をExcelで作成してみました。直線的に見えますが、そうではないようです。
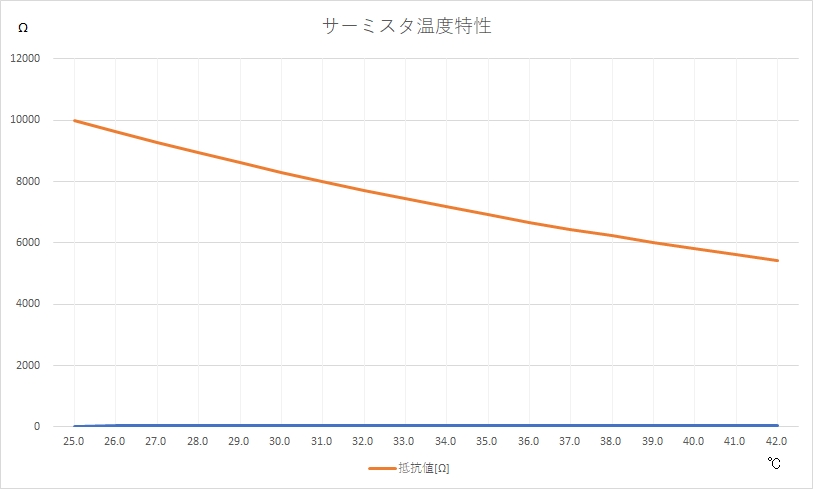
抵抗による分圧の計算方法
今度はサーミスタの抵抗値から、Arduinoマイコンが測定できる電圧に変換する回路(分圧回路)を検討します。ここではもうひとつ抵抗を使います。
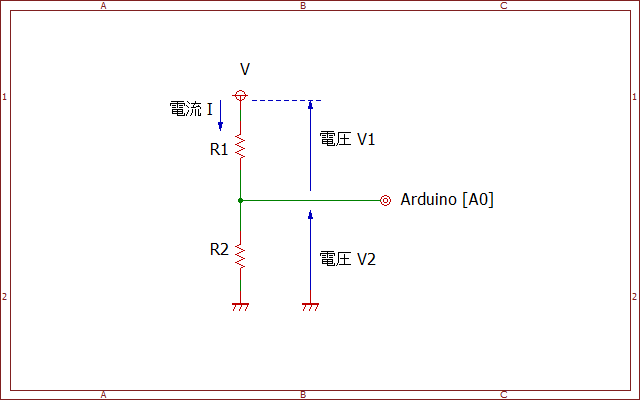
電流 $I$ は $R_1$ と$R_2$ の共通に流れるので、オームの法則から $I=\cfrac{V_1}{R_1}=\cfrac{V_2}{R_2}$ となり、$V_1$ と $V_2$ を足せば $V$ になります。この二つの式から $V_2$ を求めます。
(1) \(\cfrac{V_1}{R_1}=\cfrac{V_2}{R_2}\)
(2) \(V=V_1+V_2、V_2を移項して V_1=V-V_2\)
(1) 式と (2) 式から $V_2$ を求めます。
\(\cfrac{V-V_2}{R_1}=\cfrac{V_2}{R_2}\)
\(R_1V_2=R_2(V-V_2)=R_2V-R_2V_2\)
\(R_1V_2+R_2V_2=R_2V\)
\(V_2(R_1+R_2)=R_2V\)
\(V_2=\cfrac{R_2}{R_1+R_2}V\)
$V_2$ を求めることができました。実際の回路では、$R_2$ にサーミスタ抵抗をおきます。サーミスタ抵抗は温度が上昇すれば抵抗値は小さくなっていくので、この回路では $V_2$ も小さくなっていきます。
温度測定
測定した温度がわかるように、I2C接続キャラクタLCDモジュール(ACM1602NI-FLW-FBW-M01)を使い、ブレッドボードで組みました。Arduinoマイコンの電源は、パソコンのUSBポートから取っています。ブレッドボードについては、ブレッドボードの使い方を参照ください。
回路図
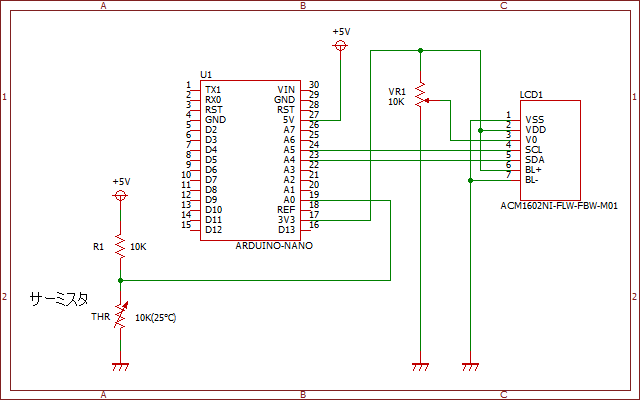
プログラム
//Minoyalab なんちゃって体温計
//
#include <math.h>
#include <Wire.h> //I2C
#include <wI2cLcdACM1602.h> //LCD
wI2cLcdACM1602 lcd;
int AN0 = 0;
void setup () {
Serial.begin(9600); //9600bps
Wire.begin(); // I2C初期化
lcd.begin(); // LCD初期化
lcd.clear(); // 全クリア
lcd.noBlink(); // カーソル点滅なし
lcd.noCursor(); // カーソル表示なし
}
void loop () {
int B = 3380; //B定数
int R1 = 10000; //10KΩ
int T0 = 25; //基準温度25℃
int val; //アナログ値
float V0; //アナログ値電圧換算
float THR; //サーミスタ抵抗
float TEMP; //温度
val = analogRead(AN0); //アナログ値読込み
V0 = val*5.0/1023.0; //アナログ値から電圧換算
THR = 10000.0*V0/(5.0-V0); //電圧値からサーミスタ抵抗値換算
TEMP = 1/(log(THR/R1)/B+1/(T0+273.0))-273.0; //温度計算
lcd.setCursor(0,0);
lcd.print(TEMP,1); //温度表示
lcd.setCursor(5,0);
lcd.print('C');
delay(1000); //1秒待つ
}
Arduinoのアナログ入力(AN0)は、0から1023の分解能(10ビット)があり、ひとつの値は 5V÷1023=0.00489Vになります。
電子体温計の測定範囲は 32.0℃~42.0℃なので、TEMP ℃にその値を入れてデジタル値を計算してみました。
| TEMP ℃ | THR Ω | AN0 V | デジタル値 |
|---|---|---|---|
| 32.0 | 7708 | 2.176 | 445 |
| 33.0 | 7434 | 2.132 | 436 |
| 34.0 | 7171 | 2.088 | 427 |
| 35.0 | 6919 | 2.045 | 418 |
| 36.0 | 6678 | 2.002 | 410 |
| 37.0 | 6446 | 1.960 | 401 |
| 38.0 | 6224 | 1.918 | 392 |
| 39.0 | 6011 | 1.877 | 384 |
| 40.0 | 5807 | 1.837 | 376 |
| 41.0 | 5610 | 1.797 | 368 |
| 42.0 | 5422 | 1.758 | 360 |
1秒ごとに測定しています。ちょっと見にくいですが、ブレッドボードの中央にある小さい水色の粒が、サーミスタです。

電子体温計を指で挟んで温度測定、33.6℃を表示しています。
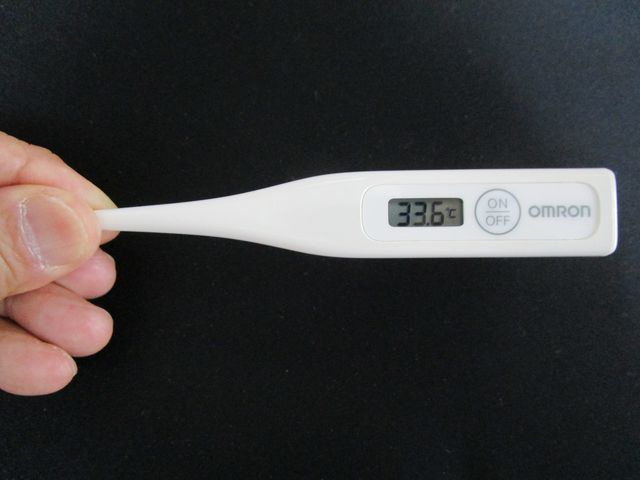
サーミスタを指で挟んで温度測定、電子体温計と同じ33.6℃を表示しました。

押さえる指の面積で測定値は変化しますが、電子体温計と同じ測定値が出たのでビックリしました。
考察
電子体温計の精度は、小数点以下1桁の 0.1℃になっています。
Arduinoマイコンのアナログ入力分解能は1023、5V電源から取っているので最小値は0.00489Vになります。
サーミスタ抵抗の温度特性は直線的に変化しませんが、例えば 32.0℃から33.0℃の電圧値の差は0.0449V、これを10で割ると0.00449V、最小値の0.00489Vより小さくなり、0.1℃の温度精度は出ないことになります。
これを解決するためには、オペアンプを利用した差動増幅回路の出番となりますが、今度のときにでも考えてみようと思います。
サーミスタ部分を保護して全体的に小さくし、脇で検温しようかと考えましたが、電子体温計が流通するまで待つことにします。あくまでも確認用の目安ですね。
色々と調べると「ディジタル体温計を設計する上での重要な検討事項」という記事もありました。
そういえば毎日、何気に使っている電子体温計の校正はどうするのかな?と思ったり、改めて仕様書をよく読むと、防水性、EMC適合、RoHS対応などが出てきます。
電子体温計に限らず他の製品もそうだと思いますが、本当にものづくりは奥深いなぁ~と思いました。
早く新型コロナウイルスが終息して、いつもの日常が戻り、卓球を楽しみたいですね。

